10223. The Settlers of Catan

Within Settlers of Catan, the 1995 German game of the year, players attempt to dominate an island by building roads, settlements and cities across its uncharted wilderness.

You are employed by a software company that just has decided to develop a computer version of this game, and you are chosen to implement one of the game’s special rules:

When the game ends, the player who built the longest road gains two extra victory points.

The problem here is that the players usually build complex road networks and not just one linear path. Therefore, determining the longest road is not trivial (although human players usually see it immediately).

Compared to the original game, we will solve a simplified problem here: You are given a set of nodes (cities) and a set of edges (road segments) of length 1 connecting the nodes. The longest road is defined as the longest path within the network that doesn’t use an edge twice. Nodes may be visited more than once, though.

Input. Contains one or more test cases. The first line of each test case contains two integers: the number of nodes n (2 ≤ n ≤ 25) and the number of edges m (1 ≤ m ≤ 25). The next m lines describe the m edges. Each edge is given by the numbers of the two nodes connected by it. Nodes are numbered from 0 to n − 1. Edges are undirected. Nodes have degrees of three or less. The network is not necessarily connected. Input will be terminated by two values of 0 for n and m.

Output. For each test case, print the length of the longest road on a single line.

Sample input	Sample output
3 2 0 1 1 2 15 16 0 2 1 2 2 3 3 4 3 5 4 6 5 7 6 8 7 8 7 9 8 10 9 11 10 12 11 12 10 13 12 14 0 0	2 12

SOLUTION

graphs – backtracking

Algorithm analysis

Run the depth first search from each vertex. Generate all possible paths using backtracking. The limitation on the number of vertices (n ≤ 25) allows you to keep within the time limit. Find the length of the longest path.

Example

In the second sample the longest path has the length 12.

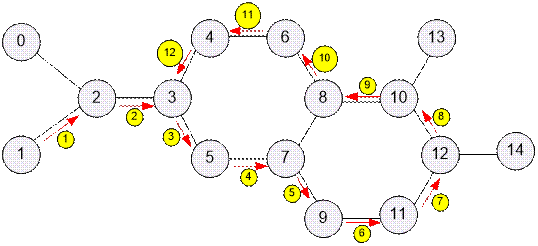
Algorithm realization

Declare the adjacency matrix mas of the graph.

#define MAX 26

int mas[MAX][MAX];

Enter the vertex i. The current distance from the starting vertex to i is depth.

void run(int i, int depth)

{

The variable best maintains the value of the longest path.

if (depth > best) best = depth;

Find into which vertex j can we go from i.

for (int j = 0; j < n; j++)

if (mas[i][j])

{

Delete the edge (i, j) and continue search from the vertex j.

mas[i][j] = mas[j][i] = 0;

run(j, depth + 1);

Upon return from the function run restore the edge (i, j).

mas[i][j] = mas[j][i] = 1;

}

}

The main part of the program. Process several test cases.

while (scanf("%d %d", &n, &m), n + m)

{

memset(mas, 0, sizeof(mas));

Read the input data. Construct the graph.

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

mas[a][b] = mas[b][a] = 1;

}

Run the depth first search from each vertex. Vertices are numbered from 0 to n – 1. In the variable best compute the maximum length of the path.

best = 0;

for (i = 0; i < n; i++)

run(i, 0);

Print the answer.

printf("%d\n", best);

}

Java realization

import java.util.*;

public class Main

{

static int g[][] = new int[26][26];

static int n, m, best;

static void run(int i, int depth)

{

if (depth > best) best = depth;

for (int j = 0; j < n; j++)

if (g[i][j] == 1)

{

g[i][j] = g[j][i] = 0;

run(j, depth + 1);

g[i][j] = g[j][i] = 1;

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while(true)

{

n = con.nextInt();

m = con.nextInt();

if (n == 0 && m == 0) break;

for (int i = 0; i < 26; i++)

Arrays.fill(g[i], 0);

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = g[b][a] = 1;

}

best = 0;

for (int i = 0; i < n; i++)

run(i, 0);

System.out.println(best);

}

con.close();

}

}